Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Gravitation - Planetenbahnen
In diesem Abschnitt wollen wir die Bewegung eines Planeten unter den Einfluss eines Zentralgestirns (der Sonne) modellieren. Die Kräfte, die die beiden Körper aufeinander ausüben, werden durch Newtons Gravitationsgesetz beschrieben. Wir betrachten ein vereinfachtes Modell, bei dem z.B. die große Masse M der Sonne ruht, dennoch sind wir in der Lage anhand dieses Modells z.B. das zweite Keplersche Gesetz zu überprüfen.
Der Abschnitt Einführung in die Numerik sollte bereits behandelt worden sein, um diesen Abschnitt verstehen zu können. Des Weiteren sollte die Behandlung des Inhaltes Java Applet nicht zu lange zurückliegen.
Physikalische Grundlagen
Das Gravitationsgesetz - Kräfte sind Vektoren
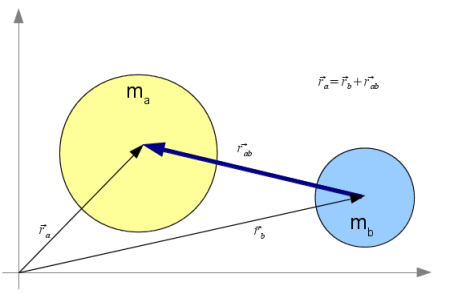
Das Newtonsche Gravitationsgesetz beschreibt die Wechselwirkungskraft zwischen zwei Massenpunkten (hier $m_a$ und $m_b$). Der vektorielle Charakter der Kraft muss in der Modellierung berücksichtigt werden. Mit $\overrightarrow{F}_{ab} $ bezeichnen wir die Kraft, die von der Masse $m_a$ auf $m_b$ ausgeübt wird. Dann gilt nach Newton:
\begin{equation} \overrightarrow{F_{ab}} = G\; m_a\; m_b \frac{\overrightarrow{r_a} - \overrightarrow{r_b}}{ | \overrightarrow{r}_a - \overrightarrow{r_b} |^3} \end{equation}
Hier bezeichnet $G =6.67 \cdot 10^{-11} m^3 kg^{-1} s^{-2}$ die Gravitationskonstante. Wir erwähnen noch, dass die Kraft proportional zum Quadrat des Abstandes (~ 1/r²) ist und dass sie entlang der Verbindungsgeraden der beiden Massen gerichtet ist (das ist eine Eigenschaft, die sogenannte Zentralkräfte aufweisen).
Die obige Gleichung (Gl. 1) lässt sich ein wenig vereinfachen, wenn man davon ausgeht, dass sich die Masse $m_a$ im Nullpunkt des Koordinatensystems befindet (dann ist nämlich $r_a = 0$ ). Außerdem lassen wir die Indizes weg:
\begin{equation} \overrightarrow{F} = -G\; \frac{m_a\; m_b}{r^2} \cdot \frac{\overrightarrow{r}}{r}\end{equation}
Dabei ist $\frac{\overrightarrow{r}}{r}$ der Einheitsvektor in Richtung von $\overrightarrow{r}$. In dieser Form begegnet man dem Gravitationsgesetz häufig.
Das 2. Newtonsche Axion
Vollständigkeitshalber notieren wir noch kurz das 2. Newtonsche Axiom. Es besagt, dass Kraft gleich Masse mal Beschleunigung ist. $$\overrightarrow{F}= m \cdot \overrightarrow{a} $$
Implementierung in Java
Wir wollen die Bewegung eines Planeten, der um die Sonne kreist, mit Java modellieren. Dafür brauchen wir im Grunde lediglich eine Tabelle, in der die Position (X- und Y-Koordinaten) für verschiedene Zeitpunkte eingetragen ist. Jedes Koordinatenpaar (x|y) wird dann graphisch dargestellt.
| X Position | Y Position | Zeitpunkt |
|---|---|---|
| $x(t_0$) | $y(t_0)$ | $t_0$ |
| $x(t_1$) | $y(t_1)$ | $t_1$ |
| $x(t_2$) | $y(t_2)$ | $t_2$ |
| ….. | ….. | … weitere simulierte Datenpunkte |
| $x(t_n$) | $y(t_n)$ | $t_n$ |
Tabelle 1: Fiktive Tabelle zur Darstellung der Planetenbahn
Es stellt sich also die Frage, wie wir die benötigten Koordinaten erzeugen können.
Modellbeschreibung
Die Planetenbahnen werden durch das Newtonsche Gesetz beschrieben.
Die Kraft F besitzt als Vektor drei Komponenten F=($F_x$,$F_y$,$F_z$). Da die Bewegung aber nur in der Ebene stattfindet, brauchen wir lediglich zwei der drei Komponenten berücksichtigen, d.h. wir setzen die Komponente $F_z = 0$. Mit $m_a = M$ bezeichnen wir ab jetzt die Masse der Sonne und mit $m_b=m$ die des Planeten.
Die beiden resultierenden Gleichungen für die X- und Y-Komponente der Gravitationskraft lauten dann:
\begin{equation} m\cdot a_x = m\cdot\frac{dv_x}{dt} = - G\cdot m\cdot M\frac{x}{r^3}\end{equation}
\begin{equation} m\cdot a_y = m\cdot\frac{dv_y}{dt} = - G\cdot m\cdot M\frac{y}{r^3}\end{equation}
Mit $a_x$ bezeichnen wir die X-Komponente der Beschleunigung und mit $v_x$ wird die X-Komponente der Geschwindigkeit bezeichnet. Dementsprechend ist x die erste Komponente des Vektors r. Entsprechendes gilt auch für die zweite Zeile mit y. Der Abstand des Planeten von der Sonne ist
\begin{equation} r=\sqrt{x^2 + y^2} \end{equation}
Diese Gleichung diskretisieren wir jetzt, um die Geschwindigkeiten im nächsten Iterationsschritt zu erhalten: \begin{equation} v_x(t + \Delta t) = v_x(t) - (G M \frac{x}{r^3}) \Delta t \end{equation} \begin{equation}v_y(t + \Delta t) = v_y(t) - (G M \frac{y}{r^3}) \Delta t \end{equation}
Für die Bahnkoordinaten verwenden wir den Euler-Cromer-Algorithmus \begin{equation} x(t + \Delta t) = x(t) + v_x(t + \Delta t) \Delta t \end{equation} \begin{equation} y(t + \Delta t) = y(t) + v_y(t + \Delta t) \Delta t \end{equation}
Heuristische Herleitung
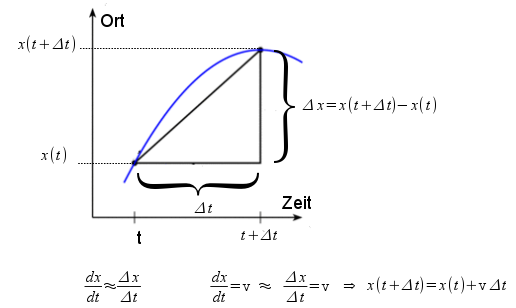 Die Diskretisierung entspricht einem Übergang vom Differentialquotienten zum Differenzenquotienten. Die Schrittweite Δt darf dabei nicht zu groß gewählt werden.
Die Diskretisierung entspricht einem Übergang vom Differentialquotienten zum Differenzenquotienten. Die Schrittweite Δt darf dabei nicht zu groß gewählt werden.
Die letzten Gleichungen (Gl. 8 und Gl. 9) liefern uns die Positionen (x und y) in Abhängigkeit einer gewählten Schrittweite (Δt).
 Diese Gleichungen benötigen, wie alle Differentialgleichungssysteme, genaue Anfangsbedingungen, um überhaupt mit der Berechnung starten zu können. Umgekehrt legen diese Anfangsbedingungen die Bahn des Planeten dann aber auch eindeutig fest. (siehe auch Abschnitt „Einführung in die Numerik“)
Diese Gleichungen benötigen, wie alle Differentialgleichungssysteme, genaue Anfangsbedingungen, um überhaupt mit der Berechnung starten zu können. Umgekehrt legen diese Anfangsbedingungen die Bahn des Planeten dann aber auch eindeutig fest. (siehe auch Abschnitt „Einführung in die Numerik“)
Die Anfangsbedingungen sind die Orte (Positionen x(0) und y(0)) zum Startzeitpunkt $t=0$ und die Geschwindigkeiten ($v_x(0)$,$v_y(0)$).