Hopfield-Netze sind sogenannt Feedback-Netze (Netze mit Rückkopplung). Bei einem Hopfield-Netz existiert nur eine Schicht, die gleichzeitig als Ein- und Ausgabeschicht ist.
Die Gewichte \(w_{ij} \) sind symmetrisch, außerdem sind alle \(w_{ii} = 0\).

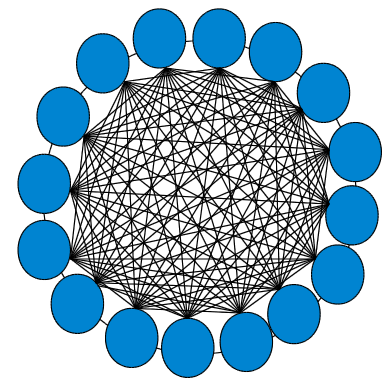
Die Abbildung zeigt ein Hopfield-Netz mit 16 Neuronen.
Alle Neuronen sind mit allen anderen Neuronen verbunden, aber kein Neuron ist mit sich selbst verbunden.
Für Hopfieldnetze gilt, dass die Verbindungsstärken $w_{ij}$ zwischen dem Neuron xi und dem Neuronxj genauso groß ist, wie zwischen Neuron $x_j$ und dem Neuronxi, d.h, für ein Hopfield Netz gilt: $w_{ij} = w_{ji}$. Die Tatsache, dass kein Neuron mit sich selbst verbunden ist, bedeutet, dass $w_{ii} = 0$ gilt.

Das Hopfield Netz ist ein Netz mit Rückkopplung (Feedback-Netz). Es besitzt nur eine Schicht, welche gleichzeitig als Ein- und Ausgabeschicht zur Verfügung steht.
Weiterhin sind die benötigten Vektoren für Ein- und Ausgabe gleich lang (autoassoziative Mustererkennung).
Die Neurone können die Werte 1 und -1 annehmen, die alle, bis auf $w_{ii}=0$, miteinander in Verbindung stehen. Bei rückgekoppelten Netzen müssen die Zustände der Neurone solange neu berechnet werden, bis das Netz in einem Ruhezustand ist (konvergiert), d.h. bis sich keine Änderung der Aktivierungszustände mehr ergeben.

Die synaptischen Gewichte sind symmetrisch, d.h. es gilt: \begin{equation} w_{ij}= w_{ji}\;\; \text{mit}\;\; w_{ii} = 0\end{equation}

Wie viele Muster kann man jetzt mit einem Hopfield-Netz speichern?

Die Speicherkapazität ist abhängig von der Zahl der Neuronen N im Netzwerk. Umso mehr Neuronen zur Verfügung stehen, desto mehr Muster M können zuverlässig gespeichert und wiedergegeben werden.

• M ~ N

Abschätzungen ergeben:

• M ≈ 0.13 · N bis M ≈ 0.15 · N

Angenommen wir haben ein Netz mit 100 Neuronen zur Verfügung, dann können wir 13 Muster speichern. Dies setzt allerdings voraus, dass sich die Muster auch gut unterscheiden lassen, d.h. die Muster dürfen einander nicht zu ähnlich sein.
Da wir Muster durch Vektoren repräsentieren, bedeutet das, dass die Vektoren möglichst orthogonal (senkrecht) aufeinander stehen sollten. Unter orthogonalen Mustern verstehen wir Muster, die sich von allen Möglichkeiten am stärksten unterscheiden.

Hopfield-Netze sind gekennzeichnet durch die Aktivierungsfunktion:

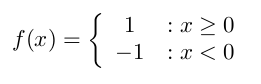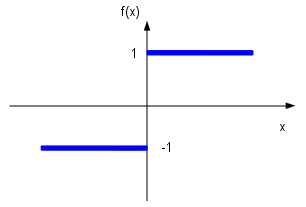Wenn x größer oder gleich null ist, nimmt f den Funktionswert 1 an. Ansonsten ist der Funktionswert -1.	Graphische Darstellung der Aktivierungsfunktion.

Dies ist eine Schwellenwertfunktion. Jedes Neuron $x_i$ berechnet zunächst die gewichtete Summe aller Eingangsverbindungen. Die Ausgabe beträgt 1, wenn die Aktivierung größer als der Schwellenwert ist. Sie nimmt den Wert -1 an, wenn die Aktivierung kleiner als der Schwellenwert ist.

Um den nächsten Zustand der Neurone zu ermitteln, gibt es zwei grundsätzlich verschiedene Verfahren:

• Asynchrone Aktivierung
  • Zu jedem Zeitpunkt ändert nur ein einziges Neuron seinen Aktivierungszustand (dieses Neuron wird zufällig ausgewählt)

• Synchrone Aktivierung
  • Alle Neurone ändern ihren Zustand gleichzeitig (paralleles Update)

Unabhängig von diesen beiden Verfahren, muss zuerst die Netzeingabe $net_i$ des Neurons bestimmt werden, welches 'upgedatet' werden soll. Mithilfe dieser Netzeingabe kann dann anhand der Aktivierungsfunktion der nächste Zustand bestimmt werden.